同构 ¶
同构¶
此示例展示了如何使用 isomorphic()检查小图之间的同构。
首先,我们生成三个不同的图
import igraph as ig
import matplotlib.pyplot as plt
# Create Graphs
g1 = ig.Graph([(0, 1), (0, 2), (0, 4), (1, 2), (1, 3), (2, 3), (2, 4), (3, 4)])
g2 = ig.Graph([(4, 2), (4, 3), (4, 0), (2, 3), (2, 1), (3, 1), (3, 0), (1, 0)])
g3 = ig.Graph([(4, 1), (4, 3), (4, 0), (2, 3), (2, 1), (3, 1), (3, 0), (1, 0)])
要检查它们是否同构,我们运行
# Check isomorphism
print("Are the graphs g1 and g2 isomorphic?")
print(g1.isomorphic(g2))
print("Are the graphs g1 and g3 isomorphic?")
print(g1.isomorphic(g3))
print("Are the graphs g2 and g3 isomorphic?")
print(g2.isomorphic(g3))
最终输出是
Are the graphs g1 and g2 isomorphic?
True
Are the graphs g1 and g3 isomorphic?
False
Are the graphs g2 and g3 isomorphic?
False
注意
图同构是一种等价关系,即如果 g1 ~ g2 且 g2 ~ g3,则自动 g1 ~ g3。因此,我们可以跳过示例中的最后一次检查。
我们可以绘制图表来了解问题
# Plot graphs
visual_style = {
"vertex_color": "lightblue",
"vertex_label": [0, 1, 2, 3, 4],
"vertex_size": 0.4,
}
fig, axs = plt.subplots(1, 3)
ig.plot(
g1,
layout=g1.layout("circle"),
target=axs[0],
**visual_style,
)
ig.plot(
g2,
layout=g1.layout("circle"),
target=axs[1],
**visual_style,
)
ig.plot(
g3,
layout=g1.layout("circle"),
target=axs[2],
**visual_style,
)
fig.text(0.38, 0.5, '$\simeq$' if g1.isomorphic(g2) else '$\\neq$', fontsize=15, ha='center', va='center')
fig.text(0.65, 0.5, '$\simeq$' if g2.isomorphic(g3) else '$\\neq$', fontsize=15, ha='center', va='center')
plt.show()
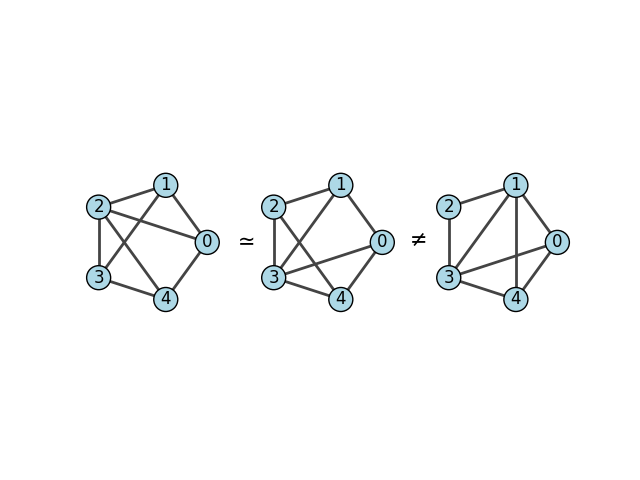
三个要比较同构的图¶