python-igraph 手册

用于从 Python 使用 igraph

拓扑排序 ¶

拓扑排序¶

此示例演示了如何在有向无环图 (DAG) 上获取拓扑排序。有向图的拓扑排序是基于有向边隐含的优先级的线性排序。当且仅当图没有任何环时，它才存在。在 igraph 中，我们可以使用 topological_sorting() 来获取顶点的拓扑排序。

import igraph as ig

# generate a directed acyclic graph (DAG)
g = ig.Graph(
    edges=[(0, 1), (0, 2), (1, 3), (2, 4), (4, 3), (3, 5), (4, 5)],
    directed=True,
)
assert g.is_dag

# g.topological_sorting() returns a list of node IDs
# If the given graph is not DAG, the error will occur.
results = g.topological_sorting(mode='out')
print('Topological sort of g (out):', *results)

results = g.topological_sorting(mode='in')
print('Topological sort of g (in):', *results)

topological_sorting() 有两种模式。'out' 是默认模式，它从入度等于 0 的节点开始。相反，模式 'in' 从出度等于 0 的节点开始。

上面代码的输出是

Topological sort of g (out): 0 1 2 4 3 5
Topological sort of g (in): 5 3 1 4 2 0

我们可以使用 indegree() 来查找节点的入度。

import igraph as ig

# generate directed acyclic graph (DAG)
g = ig.Graph(edges=[(0, 1), (0, 2), (1, 3), (2, 4), (4, 3), (3, 5), (4, 5)],
            directed=True)

# g.vs[i].indegree() returns the indegree of the node.
for i in range(g.vcount()):
    print('degree of {}: {}'.format(i, g.vs[i].indegree()))

'''
degree of 0: 0
degree of 1: 1
degree of 2: 2
degree of 3: 3
degree of 4: 4
degree of 5: 5
'''

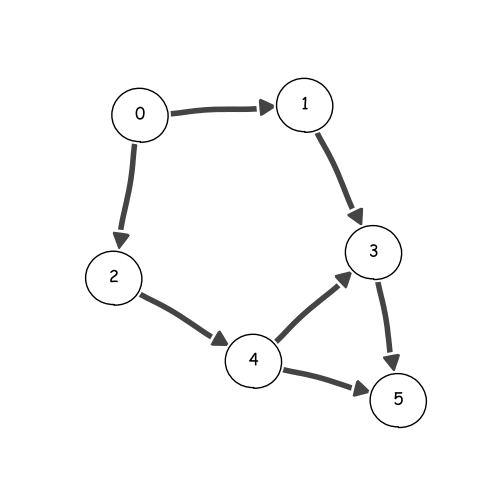
Topological sort of a directed acyclic graph (DAG) — 具有拓扑排序的图 g。¶

我们可以很容易地绘制拓扑排序后的图，如下所示

import igraph as ig
import matplotlib.pyplot as plt


# generate a directed acyclic graph (DAG)
g = ig.Graph(
    edges=[(0, 1), (0, 2), (1, 3), (2, 4), (4, 3), (3, 5), (4, 5)],
    directed=True,
)

# visualization (use xkcd style for a different flavor)
with plt.xkcd():
    fig, ax = plt.subplots(figsize=(5, 5))
    ig.plot(
            g,
            target=ax,
            layout='kk',
            vertex_size=0.3,
            edge_width=4,
            vertex_label=range(g.vcount()),
            vertex_color="white",
        )